虽然像差曲线图可以很好地给光学设计者提供一个镜头的性能,但是通常,特别是对镜头的使用者或评定者,非常需要一个客观的标准。
调制传递函数(MTF)就是这样一个广泛使用的标准,其用于非相干光成像的评价,其关注的是像的对比度或锐度。
实际上,现代许多镜头直接以 MTF 性能来衡量好坏。
如图1所示,考虑一个光学系统对强度正弦分布的光栅成像。对于非相干光成像,可以看出,像的强度也是正弦分布,但是对比度下降。
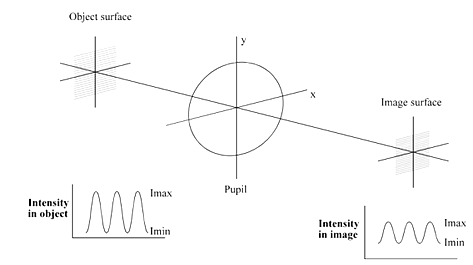
图1 一个光学系统的物像对比
MTF 是像的对比度除以物的对比度;很显然,它是空间频率的函数,在光学设计中经常使用 MTF 关于空间频率(通常单位是“线对/mm”)的函数图。
光学传递函数的定义为:

严格来说,我们应该区分光学传递函数(OTF)和调制传递函数(MTF)。
OTF 是一个矢量,其包括像的相位和振幅,其中振幅就是 MTF。
实际上,光学设计主要考虑的就是 MTF。而相位项,有时候也称为相位传递函数(PTF),表示实际正弦像相对理想正弦像的偏移,这个偏移用相位角随空间频率的变化函数表示。若相位超过 180°,那么 MTF 就可能是负的。这表示相位逆转,这种逆转会导致像的对比度也逆转。现实中,许多镜头的高频可能会出现这种情况。
对于非相干光照明的系统,其 MTF 可以用线扩散函数的 Fourier transform 求得。通常,MTF是用这种方法求得。
其中, D(s)=OTF,A=光瞳区域,S是两个光瞳重叠区域,W波前像差,s是简化的空间频率,等于fλ/NA,NA是数值孔径。
在几何光学近似中,我们假设λ接近于零,因此 MTF(子午方向)为:
这是对整个光瞳进行积分,实践上,可以用简单的求和来近似求解。
因为我们不仅需要知道弧矢方向的,而且还需要知道子午方向的MTF,所以求解弧矢方向的 MTF 用下式:
追迹大量的(通常超过 100 条)光线是很方便的,但是求和计算的时候,只考虑实际通过系统的光线。我们还要对多种波长的光线进行追迹,求和时波长的权重可以不同。
很容易给几何 MTF 添加一个校正因子,只要把几何 MTF 乘以理想系统的衍射 MTF 就行。这样的结果使得几何 MTF,不仅在大像差系统是精确的,而且在小像差系统也是精确的。但是,对于中等像差,几何MTF 通常会给出令人失望的结果。
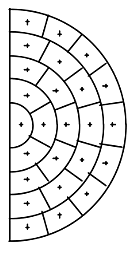
现在,我们要决定追迹多少环的光线。按图2的方式取光线,可以看出半圆中每个小区域的面积都相等。很容易看出,若有n环的光线, 则总光线数是2n 。当光学系统是对称的(关于子午y面对称),为了节约时间,程序不需要计算x负方向的光线。
有限光瞳口径的镜头对正弦物成像时,其衍射 MTF 的极限频率为:
例如对于一个f/2的镜头,其数值孔径NA为0.25,当波长λ是0.0005 mm时,截止频率为:
这个频率对应空间周期为 0.001 mm(1 μm)的光栅,但是注意,这个频率对应的 MTF值是零。对于 500 / cycles mm ,理想镜头的 MTF 约为 40% ,所以使用f/2,这是一个更为实际的频率。
用于 ZEMAX 里的 MTF,既作为一个评价工具,又作为一个优化手段。
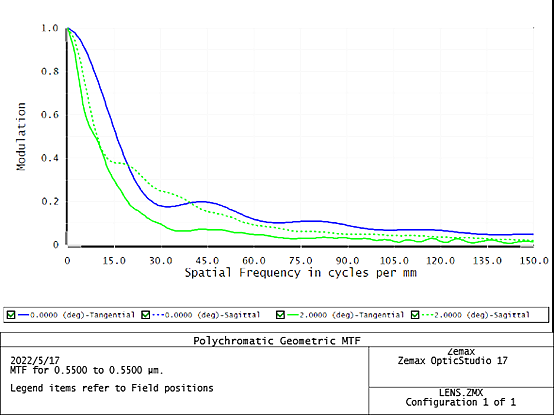
上图中,总共有四条曲线,两条是子午MTF曲线,另两条是弧矢MTF曲线,其中0°视场的子午MTF曲线弧矢MTF曲线是重合的;而2°视场的子午MTF曲线弧矢MTF曲线差别比较大,这是因为,对于离轴情况下PSF变成了非对称的,导致了PSF沿着子午和弧矢方向的宽度和轮廓有所差别。所以与近轴(或几何)像卷积后,将导致两个方向上有一个差量。这同时意味着,在两个方向上,分辨率也是不同的。
(来源:网站,版权归原作者)



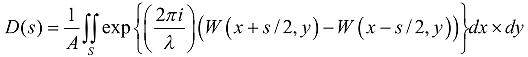
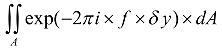
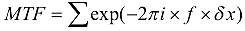
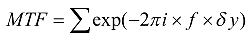
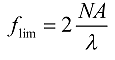
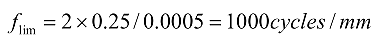

 津公网安备12010102000950号
津公网安备12010102000950号